Table des matières
Exercice 1
Prof ! Tu veux télécharger le code source , Cliquer ici 🎉
On considère la fonction ![]() définie par :
définie par :
![Rendered by QuickLaTeX.com \[\left\{\begin{array}{l}f(x)=\dfrac{x^2-9}{x-3} \quad \quad \text { si } x<3 \\ f(3)=6 \\ f(x)=\dfrac{x-3}{\sqrt{x+6}-3} \quad \text { si } x>3\end{array}\right.\]](https://guahouane.com/wp-content/ql-cache/quicklatex.com-6a7ca79cf26ea142a23ef440941226a1_l3.png)
- Étudier la continuité de la fonction
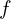 en
en 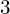 à droite, puis
à droite, puis
étudier la continuité de la fonction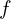 en
en 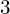 à gauche. Que peut-on dédire ?
à gauche. Que peut-on dédire ? - Montrer que
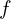 est continue sur
est continue sur 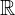 .
.
Exercice 2
On considère la fonction numérique définie par :
![]()
- Montrer que
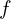 est une fonction strictement croissante sur
est une fonction strictement croissante sur 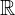 .
. - Montrer que l’équation
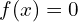 admet une solution unique
admet une solution unique ![Rendered by QuickLaTeX.com \alpha \in ]0,1[](https://guahouane.com/wp-content/ql-cache/quicklatex.com-f9889407f4d6d04fed85df33670a62de_l3.png) .
. - En utilisant la méthode de la dichotomie, donner un encadrement du nombre
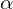 d’amplitude
d’amplitude 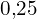 .
.
Exercice 3
On considère la fonction ![]() définie par :
définie par :
![]()
- Montrer que :
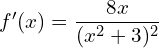 , puis déduire les variations de la fonction
, puis déduire les variations de la fonction 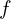 .
. - Soit
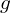 la restriction de la fonction
la restriction de la fonction 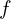 à
à 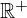 .
. - Montrer que
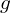 admet une finction réciproque définie sur un intervalle
admet une finction réciproque définie sur un intervalle 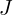 à déterminer.
à déterminer. - Calculer
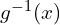 pour tout
pour tout 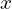 appartenant à
appartenant à 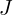 .
.
Exercice 4
Les questions sont indépendantes
- Comparer les nombres
![Rendered by QuickLaTeX.com \sqrt[5]{3}](https://guahouane.com/wp-content/ql-cache/quicklatex.com-3e19b0b7b1e2a4f966d04f4081d40e36_l3.png) et
et ![Rendered by QuickLaTeX.com \sqrt[4]{2}](https://guahouane.com/wp-content/ql-cache/quicklatex.com-cbcf78fc8cb7872a47349434e9618233_l3.png) .
. - Résoudre dans
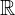 les équations suivantes :
les équations suivantes :
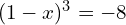
![Rendered by QuickLaTeX.com \sqrt[3]{x^{2} + 7x} = 2](https://guahouane.com/wp-content/ql-cache/quicklatex.com-e5143ca1ee3aa28ccda50a9da920b475_l3.png)
- Résoudre dans
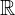 l’inéquation :
l’inéquation : ![Rendered by QuickLaTeX.com \sqrt[3]{x - 2} - 3 > 0](https://guahouane.com/wp-content/ql-cache/quicklatex.com-9e86f3fa361502c379cc74f83ae89be7_l3.png)
- Résoudre dans
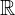 l’inéquation :
l’inéquation : ![Rendered by QuickLaTeX.com \sqrt[3]{x - 2} - 3 > 0](https://guahouane.com/wp-content/ql-cache/quicklatex.com-9e86f3fa361502c379cc74f83ae89be7_l3.png) .
. - Simplifier l’expression :
![Rendered by QuickLaTeX.com A = \dfrac{\sqrt[4]{9}\sqrt{\sqrt[3]{3}\sqrt[3]{9}}}{\sqrt[3]{81}\sqrt{\sqrt{\sqrt[3]{3}^{2}}}}](https://guahouane.com/wp-content/ql-cache/quicklatex.com-a22bc20fa3f101f6b911bc87ea83a773_l3.png)
- Calculer les limites suivantes :
Prof ! Tu veux télécharger le code source , Cliquer ici 🎉


