Table des matières
Ensemble N – Nombres pairs & impairs
Ensemble des entiers naturels : N
- Les nombres :
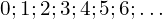 forment un ensemble appelé ensemble des entiers naturels et noté (
forment un ensemble appelé ensemble des entiers naturels et noté (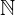 ). On écrit :
). On écrit : 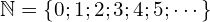 .
. - L’ensemble des entiers naturels non nuls est noté (
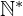 ).
).
Exemples :
- Les nombres : 10 ; 230 ; 2024 sont des entiers naturels. On écrit par exemple :
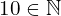 et on lit : «10 appartient à l’ensemble
et on lit : «10 appartient à l’ensemble 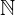 » ou encore « 10 est un élément de l’ensemble
» ou encore « 10 est un élément de l’ensemble 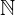 ».
». - Les nombres :
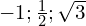 ne sont pas des entiers naturels. On écrit par exemple :
ne sont pas des entiers naturels. On écrit par exemple : 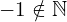 et on lit : «-1 n’appartient pas à l’ensemble
et on lit : «-1 n’appartient pas à l’ensemble 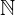 » ou encore «-1 n’est pas un élément de l’ensemble
» ou encore «-1 n’est pas un élément de l’ensemble 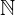 ».
».
Nombrs pairs & Nombres impairs
Soit
- On dit que
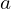 est un nombre pair s’il est multiple du nombre 2. Autrement dit, il existe un entier naturel
est un nombre pair s’il est multiple du nombre 2. Autrement dit, il existe un entier naturel 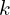 tel que :
tel que : 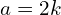 .
.
- On dit que
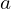 est un nombre impair s’il n’est pas pair. Autrement dit, il existe un entier naturel
est un nombre impair s’il n’est pas pair. Autrement dit, il existe un entier naturel 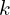 tel que :
tel que : 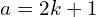 .
.
Exemples :
- Les nombres :
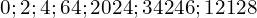 sont des nombres pairs.
sont des nombres pairs. - Les nombres :
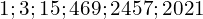 sont des nombres impairs.
sont des nombres impairs. - Motrons que le nombre
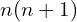 est un nombre pair avec
est un nombre pair avec 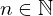 :
:
Soit ![]() un entier naturel non nul.
un entier naturel non nul.
–> Si ![]() est pair :
est pair :
alors ![]()
donc ![]()
et par suite :
![Rendered by QuickLaTeX.com \[\begin{aligned} n(n+1) \quad & =2 k(2 k+1) \\ & =2\left(2 k^2+k\right) \\ &=2 k^{\prime} \quad \text{ avec } \left(k^{\prime}=2 k^2+k \in N \right)\end{aligned}\]](https://guahouane.com/wp-content/ql-cache/quicklatex.com-e9107a337bf0fe0e4feaabb6f87aeeae_l3.png)
–> Si
alors
donc
et par suite :
![Rendered by QuickLaTeX.com \[\begin{aligned} n(n+1) & =(2 k+1) \cdot 2(k+1) \\ = & 2 \times((2 k+1) \cdot(k+1)) \\ & =2 \times\left(2 k^2+3 k+1\right) \\ &=2 \cdot k^{\prime \prime} \quad \quad \text{ avec } \left(k^{\prime \prime}=2 k^2+3 k+1 \in N \right)\end{aligned}\]](https://guahouane.com/wp-content/ql-cache/quicklatex.com-5d781c4642ed4770f41f72bad357eaba_l3.png)
D’où le résultat.
Soit
- Un entier naturel est soit pair soit impair.
- Un entier naturel est pair, si son chiffre d’unité est pair.
- Un entier naturel est impair, si son chiffre d’unité est impair.
- Déterminer la parité d’un entier naturel c’est savoir si cet entier est pair ou impair.
Opérations sur les nombres pairs et impairs
Soit 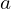 et
et 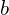 deux entiers naturels tels que :
deux entiers naturels tels que : 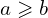 . Alors :
. Alors :
- Si
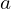 et
et 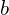 sont pairs, alors les nombres
sont pairs, alors les nombres 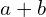 ,
, 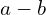 et
et 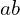 sont pairs.
sont pairs.
- Si
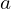 et
et 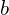 sont impairs, alors les nombres
sont impairs, alors les nombres 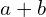 et
et 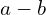 sont pairs et
sont pairs et 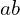 est impair.
est impair.
- Si
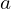 est pair et
est pair et 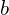 est impair, alors les nombres
est impair, alors les nombres 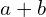 et
et 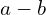 sont impairs et
sont impairs et 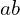 est pair .
est pair .
- Les nombres
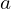 et
et 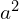 ont la même parité .
ont la même parité .
Application
- Étudier la parité des nombres suivants :
![Rendered by QuickLaTeX.com \[ 2^9+6^9 ; 17^3-5^3 ; 351 \times 208 ; 37013 \times 1375 \]](https://guahouane.com/wp-content/ql-cache/quicklatex.com-ca759b2b839fd9737d4cccb66219da60_l3.png)
- Étudier la parité des nombres suivants:


