Table des matières
Exercice 1
Soit n est un entier naturel.
-
Déterminer la parité de chacun des entiers naturels suivants :
2024 ; 7561 ; 2023 × 351 ; 1547 × 8396 ; 201913 + 144327 -
-
Déterminer les nombres pairs et les nombres impairs parmi les nombres suivants :
a = 8n + 6 ; b = 10n + 5 ; c = 4n2 + 12n + 7 ; d = 12n3 + 28n2 + 36 -
On pose : x = n(n + 1) ; y = 3n2 + 5n + 4 ; z = n2 + 7n + 11
Montrer que les nombres x et y sont pairs et le nombre z est impair.
-
Déterminer les nombres pairs et les nombres impairs parmi les nombres suivants :
-
- Développer l’expression : (n + 1)2 − n2.
- En déduire que tout nombre impair est une différence de deux carrés successifs.
- Écrire les nombres suivants comme différence de deux carrés successifs : 41 ; 59 ; 73 ; 85
-
Soit α et β deux entiers naturels tels que le nombre (α + β)2 soit pair.
Montrer que α2 + β2 est pair. -
Existe-t-il des entiers naturels pairs m, p et q vérifiant l’égalité :
p2 + q2 − 2m = 34 ?
Exercice 2
Soit n est un entier naturel.
- Montrer que le nombre 2856240 est divisible par les nombres : 4 ; 5 ; 9.
- Déterminer les multiples du nombre 23 compris entre 100 et 200.
-
Soit a, b et c des entiers naturels.
Montrer que si a divise b et c, alors a divise le nombre mb + nc pour tous entiers naturels m et n. -
- Montrer que le nombre X = 5n+3 × 3n+1 − 25 est divisible par 50.
- Montrer que le nombre n(n + 1)(n + 2) est un multiple de 3.
- Montrer que si n est impair, alors 8 divise le nombre n2 − 1.
-
On suppose dans cette question que n ≥ 4.
Montrer que si le nombre n − 4 est divisible par 5, alors le nombre n2 − 1 est aussi divisible par 5. -
- Vérifier que pour tout n ∈ ℕ :
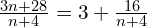 .
.
- Déterminer les valeurs de l’entier n pour lesquelles
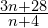 .
.
- Vérifier que pour tout n ∈ ℕ :
-
Soit x et y deux entiers naturels tels que x ≥ y.
- Montrer que les nombres x − y et x + y ont la même parité.
- Déterminer x et y sachant que x2 − y2 = 36.
-
Déterminer tous les couples (m ; n) d’entiers naturels tels que
mn + 3m + 2n = 18.
Exercice 3
-
- Déterminer l’ensemble des diviseurs de chacun des nombres 72 et 108.
- En déduire la valeur de
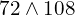 .
.
-
Soit m et n deux entiers naturels tels que :
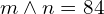 .
.
Quels sont les diviseurs communs des entiers m et n ? -
En utilisant la méthode des divisions successives, déterminer :
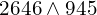 et
et 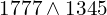 .
.
-
- Déterminer les multiples inférieurs à 200 de chacun des nombres 28 et 35.
- En déduire la valeur de
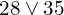 .
. - Donner cinq multiples communs supérieurs à 200 des nombres 28 et 35.
-
- Trouver tous les couples
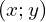 d’entiers naturels tels que :
d’entiers naturels tels que : 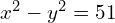 .
. - Déterminer tous les couples
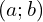 d’entiers naturels tels que :
d’entiers naturels tels que :
![Rendered by QuickLaTeX.com \[ \begin{cases} a^2 - b^2 = 7344 \\ a \wedge b = 12 \end{cases} \]](https://guahouane.com/wp-content/ql-cache/quicklatex.com-2b82fd50403acad9a5646cab66488ab8_l3.png)
- Trouver tous les couples


