Table des matières

Lorsqu’on étudie la dérivation et l’étude de fonctions, on insiste souvent sur le fait que la fonction soit dérivable sur un intervalle ouvert. Cette notion peut surprendre, surtout quand on remarque que, pour la continuité, on parle d’intervalles fermés. Cet article explique cette différence de manière pédagogique, avec des questions-réponses claires, tout en optimisant pour le SEO.

1. Qu’est-ce qu’une fonction dérivable sur un intervalle ?

La dérivabilité d’une fonction sur un intervalle signifie que sa dérivée f′(x)f'(x) existe en chaque point de cet intervalle.

Intervalle ouvert (a,b) :

  • La dérivabilité est définie localement, ce qui implique que pour tout point x∈(a,b)x \in (a, b), la fonction doit être dérivable dans un voisinage de x.
  • Comme les extrémités a et b ne sont pas incluses, il n’y a pas besoin de vérifier les conditions à ces points.

Intervalle fermé [a, b] :

Pour qu’une fonction soit dérivable sur [a, b], deux conditions supplémentaires doivent être vérifiées aux extrémités :

  1. Dérivabilité à droite de a : La dérivée doit exister en approchant a par des points strictement supérieurs (x>ax > a).
  2. Dérivabilité à gauche de b : La dérivée doit exister en approchant b par des points strictement inférieurs (x < b).

Ainsi, la dérivabilité sur [a, b] exige des vérifications aux bords, contrairement à un intervalle ouvert.

2. Pourquoi privilégie-t-on les intervalles ouverts pour la dérivabilité ?

Simplicité pédagogique :

Dans les cours, on se concentre souvent sur les intervalles ouverts (a, b) pour éviter de traiter les cas particuliers des extrémités. Cela permet d’appliquer directement les définitions et les théorèmes liés à la dérivation sans ajouter des complications inutiles.

Applications théoriques :

De nombreux théorèmes classiques, comme le théorème de Rolle ou le théorème des accroissements finis, supposent que la fonction est dérivable sur un intervalle ouvert (a, b). Cela garantit que la dérivée est bien définie sur tout l’intervalle sans ambiguïté.

Existence d’un voisinage :

La définition de la dérivée repose sur le calcul de limites en s’approchant du point considéré. Pour un point aux extrémités (a ou b), il manque un voisinage complet, ce qui rend la définition moins naturelle.

3. Mais une fonction peut-elle être dérivable sur un intervalle fermé ?

Oui, une fonction peut être dérivable sur un intervalle fermé [a, b], mais cela exige de vérifier les conditions spécifiques aux extrémités :

  • Dérivabilité à droite en a : On calcule la dérivée uniquement avec les points x > a.
  • Dérivabilité à gauche en b : On calcule la dérivée uniquement avec les points x < b.

Si ces conditions sont remplies, alors on peut parler de dérivabilité sur un intervalle fermé.

Exemple :

Considérons f(x) = x^2 sur [0, 1] :

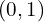  • Sur (0, 1), la fonction est dérivable partout, avec f'(x) = 2x.
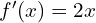  • En 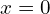x = 0, la dérivée à droite existe :

        \[ f'_d(0) = \lim_{h \to 0^+} \frac{f(0 + h) - f(0)}{h} = \lim_{h \to 0^+} \frac{h^2 - 0}{h} = 0. \]

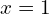  • En x = 1, la dérivée à gauche existe :

        \[ f'_g(1) = \lim_{h \to 0^-} \frac{f(1 + h) - f(1)}{h} = \lim_{h \to 0^-} \frac{(1 + h)^2 - 1}{h} = 2. \]

Ainsi, f(x) est dérivable sur [0, 1].

4. Quelle différence avec la continuité ?

La continuité est une propriété moins restrictive que la dérivabilité :

  • Pour qu’une fonction soit continue sur un intervalle fermé [a, b], il suffit qu’elle soit continue à droite en aa et à gauche en b.
  • La continuité ne nécessite pas de « taux de variation » ou de pente contrôlée, ce qui la rend plus facile à satisfaire aux extrémités.

Exemple :

La fonction |x| est continue sur [-1, 1], mais elle n’est pas dérivable en x = 0, car il y a un angle aigu (ou cuspide). La dérivée à gauche et à droite diffèrent :

  • f_g′(0)=−1
  • f_d′(0)=1

5. Questions courantes

Pourquoi la dérivabilité implique-t-elle la continuité ?

Si une fonction est dérivable en un point, alors elle est nécessairement continue en ce point. En effet, le calcul de la dérivée repose sur une limite qui nécessite la continuité. Cependant, une fonction peut être continue sans être dérivable (par exemple,|x| en x=0 ).

Les intervalles ouverts sont-ils toujours nécessaires ?

Non, pas nécessairement. On peut travailler sur des intervalles fermés si on vérifie explicitement les conditions aux extrémités (dérivées unilatérales). Les intervalles ouverts simplifient cependant les discussions théoriques et les démonstrations.

Conclusion

Parler d’intervalles ouverts pour la dérivabilité est une simplification utile, tant pour l’apprentissage que pour les applications théoriques. Cela évite les complications liées aux extrémités, où il faut vérifier les dérivées unilatérales. Toutefois, une fonction peut être dérivable sur un intervalle fermé si les conditions aux extrémités sont remplies.

Comprendre cette distinction aide à mieux maîtriser les concepts fondamentaux de l’analyse et à éviter les confusions entre continuité et dérivabilité.

Catégorisé dans :

Divers,

Taggé dans :

, , , , , , , , , , ,