Table des matières
Introduction
Représentation graphique et variations de la fonction : ![]()
Le plan est rapporté à un repère orthonormé ![]() .
.
Soit (f) la fonction numérique définie comme suit :
![]()
où
On admet les résultats suivants :
Propriété
- Il existe trois nombres réels (\alpha), (\beta) et (k) tels que :
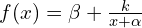 avec
avec 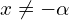 . ( la forme réduite de la fonction
. ( la forme réduite de la fonction 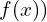 .
.
- La courbe de la fonction
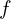 est l’image de l’hyperbole (H) d’équation
est l’image de l’hyperbole (H) d’équation 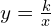 par la translation de vecteur
par la translation de vecteur 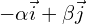 .
.
- Variations de
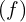 :
:

Définition
La courbe deExemple
On considère la fonction ![]()
- Écrire
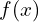 sous la forme réduite et donner le tableau de variations de
sous la forme réduite et donner le tableau de variations de 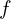 .
.
- Tracer la courbe de la fonction
 .
.
Solution
- 1. On a la forme réduite de (f(x)) :
![Rendered by QuickLaTeX.com \[f(x)=\frac{2 x+1}{x-1}=\frac{2(x-1)+3}{x-1}=2+\frac{3}{x-1} \]](https://guahouane.com/wp-content/ql-cache/quicklatex.com-3e94bc679ef1879a440a2ece51dcf94c_l3.png)
Puisque (k=3 ) alors le tableau de variations est :

- 2. Pour tracer
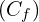 , on identifie cette forme à
, on identifie cette forme à 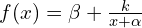 .
.
Ici, ,
, 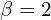 , et
, et 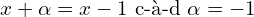 .
.
Donc,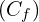 est l’image de l’hyperbole de référence (H) d’équation
est l’image de l’hyperbole de référence (H) d’équation 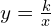 , c’est-à-dire
, c’est-à-dire 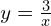 , par la translation de vecteur
, par la translation de vecteur 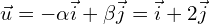
Le centre de l’hyperbole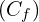 est le point
est le point 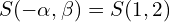 .
.
Les asymptotes de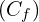 sont les droites d’équations
sont les droites d’équations 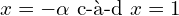 (asymptote verticale) et
(asymptote verticale) et 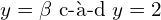 (asymptote horizontale).
(asymptote horizontale).


