Table des matières
![]() <br>
<br>
Donc, 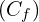 est l’image de l’hyperbole de référence (H) d’équation
est l’image de l’hyperbole de référence (H) d’équation 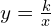 , c’est-à-dire
, c’est-à-dire 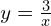 , par la translation de vecteur
, par la translation de vecteur 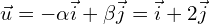
La fonction
Soit ![]() un nombre réel non nul.
un nombre réel non nul.
On considère la fonction numérique ![]() de la variable réelle
de la variable réelle ![]() définie par
définie par ![]() et (
et (![]() ) sa représentation graphique dans un repère orthonormé
) sa représentation graphique dans un repère orthonormé ![]() .
.
- Ensemble de définition :
![Rendered by QuickLaTeX.com D_f = ]-\infty, 0[ \cup ]0, +\infty[](https://guahouane.com/wp-content/ql-cache/quicklatex.com-401091b3d6a92ea1ec50cd8b96278d62_l3.png) .
. - Parité de la fonction
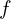 :
:
Soit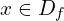 . On a :
. On a : 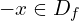 .
.
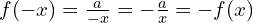 Donc
Donc 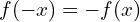 , et par suite
, et par suite 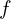 est une fonction impaire.
est une fonction impaire. - Variations de
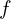 :
:
- Si
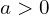 :
:
- Si
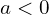 :
:
- Si
- Si
- Représentation graphique :
Puisque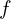 est une fonction impaire, il suffit de représenter
est une fonction impaire, il suffit de représenter 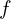 sur
sur ![Rendered by QuickLaTeX.com ]0, +\infty[](https://guahouane.com/wp-content/ql-cache/quicklatex.com-ee171d914818059b7409fa5e2660b410_l3.png) , puis on complète la courbe de la fonction
, puis on complète la courbe de la fonction 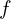 sur l’intervalle
sur l’intervalle ![Rendered by QuickLaTeX.com ]-\infty, 0[](https://guahouane.com/wp-content/ql-cache/quicklatex.com-d45f44f6ca902f742ec9e4c73b66ee5e_l3.png) en utilisant la symétrie centrale de centre
en utilisant la symétrie centrale de centre  , l’origine du repère.
, l’origine du repère.
La courbe de la fonction
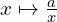 (
(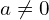 ) est appelée une hyperbole de centre
) est appelée une hyperbole de centre  , l’origine du repère, et ses asymptotes sont les droites d’équations
, l’origine du repère, et ses asymptotes sont les droites d’équations 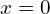 et
et 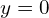 .
. :
:
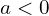 :
:
Application
Soit ![]() la fonction numérique définie sur
la fonction numérique définie sur ![]() comme suit :
comme suit : ![]() .
.
Soit ![]() sa représentation graphique dans un repère orthonormé
sa représentation graphique dans un repère orthonormé ![]() .
.
Soit (D) la droite d’équation ![]() .
.
- Représenter
 et (D) et déterminer leur intersection.
et (D) et déterminer leur intersection. - Résoudre graphiquement :
 .
.
Solution de l’application
- (D) et
 se coupent au point A d’abscisse
se coupent au point A d’abscisse 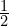 .
. - Les solutions de la double inéquation
 sont les abscisses positives des points de la courbe
sont les abscisses positives des points de la courbe  pour lesquels la droite (D) est au-dessus de
pour lesquels la droite (D) est au-dessus de  .
.
Donc, les solutions recherchées sont :![Rendered by QuickLaTeX.com S = \left]\frac{1}{2}, +\infty\right[](https://guahouane.com/wp-content/ql-cache/quicklatex.com-39e95abbf52adc68febab5c606ee7d99_l3.png) .
.
Définition : Équation cartésienne d’une droite
L’équation d’une droite avec un vecteur directeur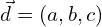 , où
, où  et
et 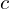 sont des nombres réels non nuls, qui passe par le point
sont des nombres réels non nuls, qui passe par le point 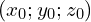 est donnée par :
est donnée par :
L’équation d’une droite avec un vecteur directeur
![]()


