Table des matières
QUESTIONS INDÉPENDANTES : (6 PTS)
- Déterminer l’ensemble de définition des fonctions suivantes : (1.5 pts)
- Étudier la parité de la fonction
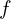 dans chacun des cas suivants : (1.5 pts)
dans chacun des cas suivants : (1.5 pts)
- Soit
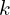 la fonction numérique définie par :
la fonction numérique définie par : 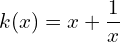 (3 pts)
(3 pts)
- Calculer les images des nombres suivants :
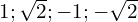
- Montrer que
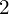 est une valeur minimale pour
est une valeur minimale pour 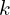 dans l’intervalle
dans l’intervalle ![Rendered by QuickLaTeX.com I = ]0 ; +\infty[](https://guahouane.com/wp-content/ql-cache/quicklatex.com-6ad19dba06f08d480358e22f5c3582b2_l3.png)
- Calculer les images des nombres suivants :
EXERCICE 1 : (7.5 PTS)
Soit ![]() la fonction numérique définie par :
la fonction numérique définie par : ![]() ,
,
et soit ![]() sa courbe représentative dans un repère orthonormé
sa courbe représentative dans un repère orthonormé ![]()
- Déterminer les points d’intersection de
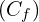 avec l’axe des abscisses. (1 pt)
avec l’axe des abscisses. (1 pt) - Vérifier que pour tout réel
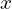 de
de 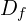 , on a :
, on a : 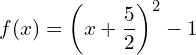 (1 pt)
(1 pt) - Déterminer les variations de
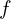 sur les intervalles
sur les intervalles ![Rendered by QuickLaTeX.com \left]-\infty, -\dfrac{5}{2}\right]](https://guahouane.com/wp-content/ql-cache/quicklatex.com-c87f1d4b4a3e6023a34672ccb43fc045_l3.png) et
et 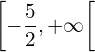 (1.5 pts)
(1.5 pts) - Tracer la courbe
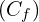 . (1.5 pts)
. (1.5 pts) - Résoudre graphiquement l’inéquation
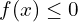 (1 pt)
(1 pt) - Déterminer le nombre de solutions de l’équation
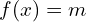 graphiquement.
graphiquement.
(Discuter suivant les valeurs du paramètre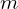 ) (1.5 pts)
) (1.5 pts)
EXERCICE 2 : (6.5 PTS)
On considère la fonction ![]() définie par :
définie par : ![]() ,
,
et soit ![]() sa courbe représentative dans un repère orthonormé
sa courbe représentative dans un repère orthonormé ![]()
- Déterminer
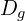 , et vérifier que pour tout
, et vérifier que pour tout 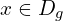 :
: 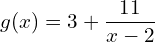 (1.5 pts)
(1.5 pts) - Déterminer les points d’intersection de
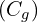 avec les axes du repère
avec les axes du repère 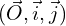 (1.5 pts)
(1.5 pts) - Étudier les variations de
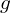 sur les intervalles
sur les intervalles ![Rendered by QuickLaTeX.com ]-\infty, 2[](https://guahouane.com/wp-content/ql-cache/quicklatex.com-9443f6f4eb6dfceceb2df6cd61902160_l3.png) ,
, ![Rendered by QuickLaTeX.com ]2, +\infty[](https://guahouane.com/wp-content/ql-cache/quicklatex.com-18966daa56a976ff6fa7981413069355_l3.png) , et dresser son tableau de variation. (2 pts)
, et dresser son tableau de variation. (2 pts) - Tracer la courbe
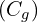 (1.5 pts)
(1.5 pts)
QUESTIONS INDÉPENDANTES : (6 PTS)
- Déterminer l’ensemble de définition des fonctions suivantes : (1.5 pts)
- Étudier la parité de la fonction
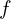 dans chacun des cas suivants : (1.5 pts)
dans chacun des cas suivants : (1.5 pts)
- Soit
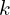 la fonction numérique définie par :
la fonction numérique définie par : 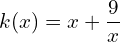 (3 pts)
(3 pts)
- Calculer les images des nombres suivants :
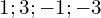
- Montrer que 6 est une valeur minimale pour
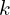 dans l’intervalle
dans l’intervalle ![Rendered by QuickLaTeX.com I = ]0 ; +\infty[](https://guahouane.com/wp-content/ql-cache/quicklatex.com-6ad19dba06f08d480358e22f5c3582b2_l3.png)
- Calculer les images des nombres suivants :
EXERCICE 1 : (7.5 PTS)
Soit ![]() la fonction numérique définie par :
la fonction numérique définie par : ![]() ,
,
et soit ![]() sa courbe représentative dans un repère orthonormé
sa courbe représentative dans un repère orthonormé ![]()
- Déterminer les points d’intersection de
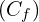 avec l’axe des abscisses. (1 pt)
avec l’axe des abscisses. (1 pt) - Vérifier que pour tout réel
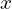 de
de 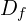 , on a :
, on a : 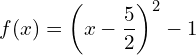 (1 pt)
(1 pt) - Déterminer les variations de
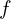 sur les intervalles
sur les intervalles ![Rendered by QuickLaTeX.com \left]-\infty, \dfrac{5}{2}\right]](https://guahouane.com/wp-content/ql-cache/quicklatex.com-1755b7478bb502a3caa169663636c94c_l3.png) et
et 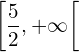 (1.5 pts)
(1.5 pts) - Tracer la courbe
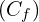 . (1.5 pts)
. (1.5 pts) - Résoudre graphiquement l’inéquation
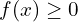 (1 pt)
(1 pt) - Déterminer le nombre de solutions de l’équation
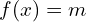 graphiquement.
graphiquement.
(Discuter suivant les valeurs du paramètre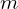 ) (1.5 pts)
) (1.5 pts)
EXERCICE 2 : (6.5 PTS)
On considère la fonction ![]() définie par :
définie par : ![]() ,
,
et soit ![]() sa courbe représentative dans un repère orthonormé
sa courbe représentative dans un repère orthonormé ![]()
- Déterminer
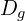 , et vérifier que pour tout
, et vérifier que pour tout 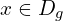 :
: 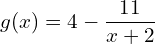 (1.5 pts)
(1.5 pts) - Déterminer les points d’intersection de
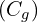 avec les axes du repère
avec les axes du repère 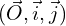 (1.5 pts)
(1.5 pts) - Étudier les variations de
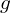 sur les intervalles
sur les intervalles ![Rendered by QuickLaTeX.com ]-\infty, -2[](https://guahouane.com/wp-content/ql-cache/quicklatex.com-73682861f16d34b51154de102ce55a41_l3.png) ,
, ![Rendered by QuickLaTeX.com ]-2, +\infty[](https://guahouane.com/wp-content/ql-cache/quicklatex.com-58bdf18b8d32d31f6e6131c68dfccc9b_l3.png) , et dresser son tableau de variation. (2 pts)
, et dresser son tableau de variation. (2 pts) - Tracer la courbe
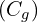 (1.5 pts)
(1.5 pts)


