Dérivabilité en un point
Nombre dérivé en un point
Définition 1
Soit
On dit qu’une fonction
![Rendered by QuickLaTeX.com \[ \boxed{\lim _{x \rightarrow x_0} \frac{f(x) - f\left(x_0\right)}{x - x_0} = \ell} \]](https://guahouane.com/wp-content/ql-cache/quicklatex.com-6f9c4de861eb7eac57d426dbefbf946d_l3.png)
Cette limite est appelée le \textbf{nombre dérivé} de ![]() en
en ![]() , noté
, noté ![]() .
.
Remarque 1
- Une autre définition équivalente de la dérivée est :
![Rendered by QuickLaTeX.com \[f^{\prime}\left(x_0\right)=\lim _{h \rightarrow 0} \frac{f\left(x_0+h\right)-f\left(x_0\right)}{h}\]](https://guahouane.com/wp-content/ql-cache/quicklatex.com-eb0cae13a57722437819cf5ca59d76e6_l3.png)
- Notez que la dérivée d’une fonction (y=f(x)) peut également être notée
![Rendered by QuickLaTeX.com \[\frac{ d y}{ d x}\]](https://guahouane.com/wp-content/ql-cache/quicklatex.com-4d923f85d7bb81e1983c8b3afb9d5006_l3.png)
qui se lit comme «la dérivée de (y) par rapport à (x ) » ou « (d y) sur (d x ) ».
Exemple 1
Soit la fonction ![]() définie comme suit :
définie comme suit :
![]()
Étudier la dérivabilité de ![]() en
en ![]() et déterminez sa dérivée en ce point.
et déterminez sa dérivée en ce point.
Pour étudier la dérivabilité de ![]() en
en ![]() , nous devons vérifier si la limite suivante existe :
, nous devons vérifier si la limite suivante existe :
![]()
On a :
![Rendered by QuickLaTeX.com \[ \begin{aligned} \lim _{x \rightarrow 3} \frac{g(x)-g(3)}{x-3} &= \lim _{x \rightarrow 3} \frac{2x+1-7}{x-3} \\ &= \lim _{x \rightarrow 3} \frac{2x-6}{x-3} \\ &= \lim _{x \rightarrow 3} \frac{2(x-3)}{x-3} \\ &= 2 \end{aligned} \]](https://guahouane.com/wp-content/ql-cache/quicklatex.com-004430231a3a26a8112711a8ff4d4878_l3.png)
Comme la limite existe et est finie, nous pouvons conclure que ![]() est dérivable en
est dérivable en ![]() .
.
Conclusion : La fonction ![]() est dérivable en
est dérivable en ![]() , et sa dérivée en ce point est de 2.
, et sa dérivée en ce point est de 2.
Interprétation géométrique
Définition 2
L’équation de la \textbf{tangente} à la courbe
![]()
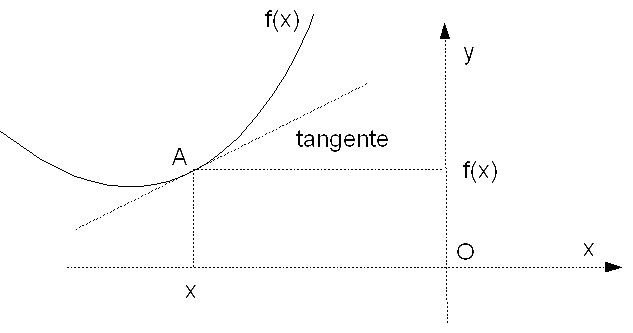
Exemple 2
Dans l’exemple précédente, on montré que la fonction ![]() est dérivable en
est dérivable en ![]() , et sa dérivée en ce point est de 2 .
, et sa dérivée en ce point est de 2 .
Donc , la courbe ![]() admet une tangente
admet une tangente ![]() en
en ![]() dont l’ equation :
dont l’ equation :
![]()
![]()
![]()
Continuité et dérivabilité
Propriété 1
- Si
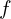 est dérivable en
est dérivable en 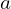 alors la fonction
alors la fonction 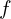 est continue en
est continue en 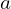 .
. - Si
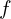 est dérivable sur un intervalle I alors la fonction
est dérivable sur un intervalle I alors la fonction 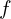 est continue sur I.
est continue sur I.
Remarque 2
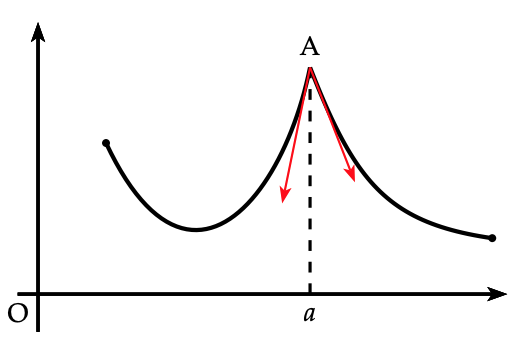
La réciproque de ce théorème est fausse. Pour s’en rendre compte, on peut s’appuyer sur une représentation graphique. Si une fonction est continue sur un intervalle, sa représentation graphique est en un seul morceau. Si la fonction est dérivable, sa représentation graphique admet une tangente en chacun de ses points. Un petit exemple :
La fonction dont la représentation est ci-contre, est bien continue en ![]() , car la courbe est en un seul morceau. Par contre, la fonction n’est pas dérivable en
, car la courbe est en un seul morceau. Par contre, la fonction n’est pas dérivable en ![]() , car la représentation admet au point A deux demi-tangentes.
, car la représentation admet au point A deux demi-tangentes.
Fonction affine tangente à f
Propriété 2
La fonction
\textsl{\underline{Autrement dit}} : \textbf{ Si }
Exemple 3
Soit ![]() la fonction définie par :
la fonction définie par : ![]()
- Déterminer
 le nombre dérivée de la fonction
le nombre dérivée de la fonction 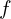 en 0 .
en 0 . - Déterminer une approximation affine au voisinage de 0 de la fonction
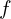 .
. - En déduire des valeurs approchées de :
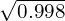 et
et 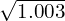
Soit ![]() la fonction définie par :
la fonction définie par : ![]()
- Déterminer
 , le nombre dérivé de la fonction
, le nombre dérivé de la fonction 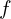 en
en 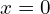 . Pour calculer
. Pour calculer  , nous pouvons utiliser la définition de la dérivée en évaluant la limite suivante :
, nous pouvons utiliser la définition de la dérivée en évaluant la limite suivante :
La fonction![Rendered by QuickLaTeX.com \[ f'(0) = \lim_{{x \to 0}} \frac{{f(x) - f(0)}}{{x - 0}} \]](https://guahouane.com/wp-content/ql-cache/quicklatex.com-2e69b61c2bbd058ae145ff67bb6f6b57_l3.png)
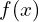 est donnée par
est donnée par  . Remplaçons dans la limite :
. Remplaçons dans la limite :
Simplifions l’expression en multipliant le numérateur et le dénominateur par le conjugué de![Rendered by QuickLaTeX.com \[ f'(0) = \lim_{{x \to 0}} \frac{{\sqrt{x+1} - \sqrt{0+1}}}{{x - 0}} \]](https://guahouane.com/wp-content/ql-cache/quicklatex.com-494cea7b3d6bf601c899c6f6c8708038_l3.png)
 :
:
En simplifiant le numérateur et le dénominateur, nous obtenons :![Rendered by QuickLaTeX.com \[ f'(0) = \lim_{{x \to 0}} \frac{{(\sqrt{x+1} - \sqrt{1})(\sqrt{x+1} + \sqrt{1})}}{{x - 0(\sqrt{x+1} + \sqrt{1})}} \]](https://guahouane.com/wp-content/ql-cache/quicklatex.com-1c8ff01a7467ca9daba5b7179b9864f7_l3.png)
Finalement, nous avons :![Rendered by QuickLaTeX.com \[ f'(0) = \lim_{{x \to 0}} \frac{{x}}{{x(\sqrt{x+1} + \sqrt{1})}} \]](https://guahouane.com/wp-content/ql-cache/quicklatex.com-aa22c71bd35818adee8c89230f63b99f_l3.png)
Évaluons cette limite en![Rendered by QuickLaTeX.com \[ f'(0) = \lim_{{x \to 0}} \frac{{1}}{{\sqrt{x+1} + \sqrt{1}}} \]](https://guahouane.com/wp-content/ql-cache/quicklatex.com-1e522b6ec64ed85f3f20eaf94ebb9e7d_l3.png)
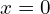 :
:
Ainsi, nous trouvons que![Rendered by QuickLaTeX.com \[ f'(0) = \frac{{1}}{{\sqrt{0+1} + \sqrt{1}}} = \frac{{1}}{{2}} \]](https://guahouane.com/wp-content/ql-cache/quicklatex.com-6d13f49655808ab038e4fc5897e5023e_l3.png)
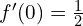 .
. - Déterminer une approximation affine au voisinage de
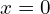 de la fonction
de la fonction 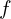 . Une approximation affine au voisinage de
. Une approximation affine au voisinage de 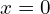 de la fonction
de la fonction 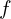 peut être obtenue en utilisant la formule de la tangente à la courbe en ce point. La forme générale de l’approximation affine est :
peut être obtenue en utilisant la formule de la tangente à la courbe en ce point. La forme générale de l’approximation affine est :
Pour notre cas, en prenant![Rendered by QuickLaTeX.com \[ L(x) = f(a) + f^{\prime}(a)(x - a) \]](https://guahouane.com/wp-content/ql-cache/quicklatex.com-183034b69fe3a6a903b8a0777287f44f_l3.png)
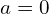 , nous obtenons :
, nous obtenons :
Donc, une approximation affine au voisinage de![Rendered by QuickLaTeX.com \[ L(x) = f(0) + f^{\prime}(0)(x - 0) = \sqrt{1} + \frac{1}{2}(x - 0) = 1 + \frac{1}{2}x \]](https://guahouane.com/wp-content/ql-cache/quicklatex.com-8e1c3b87417df9e6186229a8e8e1a843_l3.png)
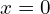 de la fonction
de la fonction 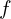 est
est 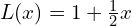 .
. - En déduire des valeurs approchées de
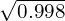 et
et 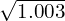 . Pour trouver des valeurs approchées de
. Pour trouver des valeurs approchées de 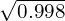 et
et 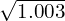 , nous pouvons utiliser l’approximation affine obtenue précédemment.En substituant
, nous pouvons utiliser l’approximation affine obtenue précédemment.En substituant 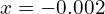 dans
dans 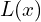 , nous obtenons :
, nous obtenons :
De même, en substituant![Rendered by QuickLaTeX.com \[ \sqrt{0.998} = \sqrt{1 - 0.002} \approx 1 + \frac{1}{2}(-0.002) = 0.999 \]](https://guahouane.com/wp-content/ql-cache/quicklatex.com-e525469759961b3288504c717e40cfa8_l3.png)
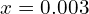 dans
dans 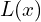 , nous obtenons :
, nous obtenons :
Donc, une valeur approximative de![Rendered by QuickLaTeX.com \[ \sqrt{1.003} = \sqrt{1 + 0.003} \approx 1 + \frac{1}{2}(0.003) = 1.0015 \]](https://guahouane.com/wp-content/ql-cache/quicklatex.com-6342b502d28416003da61c2f7264ee90_l3.png)
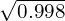 est
est 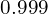 et une valeur approximative de
et une valeur approximative de 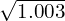 est
est 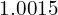 .
.
Dérivabilité à droite et à gauche
Dérivabilité à gauche et à droite d’un point
Définition 3
-
Soit
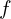 une fonction définie sur un intervalle de la forme
une fonction définie sur un intervalle de la forme  avec
avec 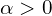 ,
, 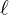 et
et 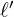 deux réels.
deux réels.
On dit que
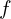 est dérivable à droite en
est dérivable à droite en 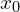 , si :
, si :
![Rendered by QuickLaTeX.com \[ \lim\limits_{x \to x_0^{+}} \frac{f(x) - f\left(x_0\right)}{x - x_0} = \ell \]](https://guahouane.com/wp-content/ql-cache/quicklatex.com-6b5b41dc948929a0409ac4e612585040_l3.png)
Cette limite est appelée le nombre dérivé de
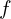 à droite en
à droite en 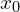 , et on le note
, et on le note  .
.
-
Soit
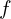 une fonction définie sur un intervalle de la forme
une fonction définie sur un intervalle de la forme ![Rendered by QuickLaTeX.com ]a - \alpha, a]](https://guahouane.com/wp-content/ql-cache/quicklatex.com-d549ee51d960f9c4ad9bef8fea15bfa6_l3.png) avec
avec 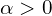 , et
, et 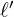 un réel.
un réel.
On dit que
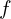 est dérivable à gauche en
est dérivable à gauche en 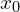 , si :
, si :
![Rendered by QuickLaTeX.com \[ \lim\limits_{x \to x_0^{-}} \frac{f(x) - f\left(x_0\right)}{x - x_0} = \ell^{\prime} \]](https://guahouane.com/wp-content/ql-cache/quicklatex.com-c454712a1a807064a1680345a967bee3_l3.png)
Cette limite est appelée le nombre dérivé de
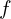 à gauche en
à gauche en 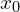 , et on le note
, et on le note 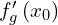 .
.
Exemple 4
Étudions la dérivabilité de la fonction ![]() à droite et à gauche de
à droite et à gauche de ![]() .
.
À droite de 0 :
Pour ![]() , la fonction
, la fonction ![]() est égale à
est égale à ![]() .
.
On a :
![]()
La limite est égale à 1,
Donc, la fonction
À gauche de 0 :
Pour
On a :
![]()
La limite est égale à -1,
Donc, la fonction
Donc, la fonction
Propriété 3
![]() est dérivable en
est dérivable en ![]() si et seulement si
si et seulement si ![]() est dérivable à droite et à gauche en
est dérivable à droite et à gauche en ![]() et
et ![]()
Interprétation géométrique
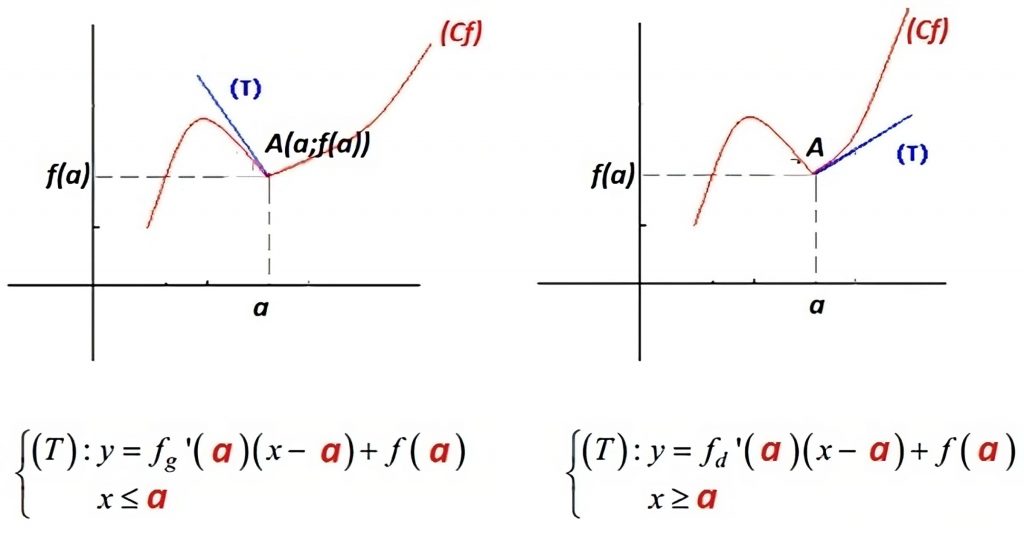
-
Si
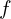 est une fonction dérivable à droite de
est une fonction dérivable à droite de 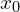 , alors sa courbe
, alors sa courbe 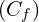 admet une demi-tangente à droite de
admet une demi-tangente à droite de 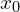
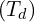 de coefficient directeur
de coefficient directeur 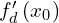 .
.
L’équation de la demi-tangente à droite de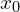
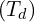 est :
est :
![Rendered by QuickLaTeX.com \[ \left(T_d\right): y = \left(x - x_0\right) f_d^{\prime}\left(x_0\right) + f\left(x_0\right) \quad \text{avec } x \geq x_0 \]](https://guahouane.com/wp-content/ql-cache/quicklatex.com-e15b8be828d512f4df8080acbed8ffa9_l3.png)
-
Si
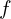 est dérivable à gauche de
est dérivable à gauche de 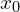 , alors sa courbe
, alors sa courbe 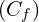 admet une demi-tangente à gauche de
admet une demi-tangente à gauche de 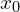
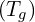 de coefficient directeur
de coefficient directeur  .
.
L’équation de la demi-tangente à gauche de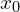
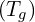 est :
est :
![Rendered by QuickLaTeX.com \[ \left(T_g\right): y = \left(x - x_0\right) f_g^{\prime}\left(x_0\right) + f\left(x_0\right) \quad \text{avec } x \leq x_0 \]](https://guahouane.com/wp-content/ql-cache/quicklatex.com-24bfc97568dc917b359417dd3ceda2de_l3.png)
Point anguleux

Interprétations géométriques



